The chemical concept of a “mole” is very important to be able to perform calculations in chemistry. Remember from your class that an atom’ atomic weight refers to the number of grams in one “mole” of that material. What exactly is a mole? And how can we use it in calculations while not confusing ourselves with all the different units and conversion factors? It’s easy to panic when you’re given so many different units to convert, and a complicated reaction to follow. What’s the easiest way to keep yourself on track?
Luckily, chemists have developed a system of record-keeping that keeps everything straight. It allows you to take small, easy-to-understand steps towards the final answer. This method is called dimensional analysis. It involves drawing a horizontal line on a piece of paper and then drawing vertical lines parallel to the horizontal line to form a sequence of blocks. It looks something like this:

You can make this line as long as you need to solve a problem. There are a few rules on how to use dimensional analysis correctly, and we’ll show you those rules with some real-world examples.

First, some definitions. A “mole” is a term used by chemists to refer to a set number of molecules. Molecules are extremely tiny, so it takes a lot of them to make one mole. Specifically, it takes \(6.022 \times 10^{23}\) molecules to equal one mole of molecules. This number \(\left(6.022 \times 10^{23}\right)\) is called Avogadro’s number, and it’s named after the scientist who developed it. The key to understanding moles is that it doesn’t matter what atom or molecule you’re looking at. If you have \(\left(6.022 \times 10^{23}\right)\) of those individual particles, you have one mole of those things. You could even apply it to non-chemical objects, like bananas. (For the record, one mole of bananas would weigh approximately 77,002,177,086,885,298,176 tons – now that’s a lot of fruit!).

Whenever you have multiple chemicals in a chemical reaction and need to calculate weight, moles come into play. Let’s take a look at how we can use moles in dimensional analysis to solve questions. Here’s an example.
Magnesium metal reacts with hydrochloric acid to form hydrogen gas and magnesium chloride, a salt. The chemical reaction scheme is: \(\mathrm{Mg}+2 \mathrm{HCl} \rightarrow \mathrm{MgC} 1_{2}+\mathrm{H}_{2}\). If you start with 1.00 ounce of magnesium and the reaction goes to completion, how many grams of \(\mathrm{MgC} 1_{2}\) do you form?
Yikes! There are four different chemicals in the reaction and two different units of weight. Even experienced chemists can become confused when they have to solve these types of questions.
Don’t panic! Thankfully, dimensional analysis allows us to break the problem up into small sections. We’ll use our graphical array of a horizontal line broken into columns by vertical lines. Let’s start out with a simpler question: 1 ounce of magnesium metal weighs how many grams? We know that by definition, an ounce of anything is equal to 28.35 grams. We can put this information into a dimensional analysis array, as shown below.

This is the first rule of dimensional analysis: put the information you’re given (the fact that we have 1 ounce of anything) in the first top block. The second rule of dimensional analysis is: always try to cancel units in top blocks, with units in bottom blocks. The third and final rule of dimensional analysis is: the top and bottom sections of an individual block must have a valid relationship. We couldn’t put “45 grams of anything” on the top of a block and “1 ounce of anything” on the bottom of that block, because by definition, 1 ounce weighs 28.35 grams.
Those are the only three rules you need to know! They’re simple, and they allow you to solve thousands of chemical equation problems. Even very complicated questions are broken down into individual steps which are easy to understand. Looking at our example above: because there is an entry of “an ounce of anything” listed on both the top and the bottom of this array, those units cancel out. The dimensional analysis array then becomes:

Everything along the top is multiplied together to give a final number for the top row. Everything along the bottom is multiplied together to give a final number for the bottom row. In the final step, we divide the final number for the top row by the final number for the bottom row and assign it the units that are leftover in the last top block. So, let’s go back to our magnesium reaction.
Because there’s an “ounce of magnesium” on both the top and the bottom, they cancel each other out. We multiply everything along the top (1 x 28.35) and divide that by 1, the number on the bottom row. The only units left are “grams of magnesium”, so we can say that 1 ounce of magnesium is equal to 28.35 grams of magnesium.
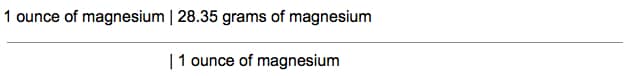
This type of unit conversion really starts to shine when you set up multiple boxes in the dimensional analysis array. We know the atomic weight of Mg from the Periodic Table: it weighs 24.31 grams per mole.

Did you see what we did there? The goal is to cancel out the top units with the bottom units. In the first step, we have to cancel out “an ounce of Mg”, so we plug in the known value for the number of grams in an ounce (28.35). Now, we need to cancel out “grams of Mg”. We know we’re going to use moles eventually (because a chemical equation is involved), so we look at the Periodic table and find that 1 mole of Mg weighs 24.31 grams. We put “grams of Mg” on the bottom to cancel out the top units in the bracket immediately to the left.
Now, just follow the usual directions. Cancel out all of the units that you can. If there is the same unit in a bracket on the top as in a bracket on the bottom, the two will cancel each other out. In this case, we have “an ounce of Mg” on the top and the bottom, so those units cancel each other. We also have “grams of Mg” on the top and the bottom, so those units cancel each other. This simplifies the array to:

We multiple all the numbers along the top, which equals 28.35. We multiple all the numbers along the bottom, which equals 24.31. We divide the top number by the bottom, which equals 1.166. Since the only units left (which should always be in the last top block) are “mole of Mg”, our answer is 1.166 mole of Mg. We started with 1 ounce of magnesium, and by using dimensional analysis, we’ve determined that 1 ounce of magnesium equals 1.166 moles of Mg.
It’s not so frightening anymore! We take tiny steps and just focus on cancelling units. We’re on a roll now, so let’s keep going and see if we can answer our original question:
Magnesium can react with hydrochloric acid to form hydrogen gas and magnesium chloride. The reaction is: \(\mathrm{Mg}+2 \mathrm{HCl} \rightarrow \mathrm{MgC} 1_{2}+\mathrm{H}_{2}\). If you start with 1.00 ounce of magnesium and the reaction goes to completion, how many milligrams of \(\mathrm{MgC}_{2}\) do you form?
We can see from the chemical equation that one mole of Mg reacts with 2 moles of HCl to form one more of \(\mathrm{MgC} 1_{2}\) and one mole of \(\mathrm{H}_{2}\). Since the question asks us to determine the amount of \(\mathrm{MgC} 1_{2}\) formed, we can ignore the HCl and \(\mathrm{H}_{2}\) and just focus on the Mg and \(\mathrm{MgC} 1_{2}\). The reaction requires 1 mole of each, so we can use that in our array.
We know that one mole of magnesium weighs 24.31 grams. We can also calculate the molecular weight of \(\mathrm{MgC} 1_{2}\) by adding up the atomic weights from the Periodic Table. \(\mathrm{MgC} 1_{2}\) has one magnesium and two chlorines, so the molecular weight of \(\mathrm{MgC} 1_{2}\) is 24.31 + 35.45 + 35.45 = 95.21 grams per mole. Let’s plug all of this information into the array using dimensional analysis, and see how far we get! Remember, you want to cancel the units on the top with the units on the bottom.

Now comes the fun part – we get to cancel all the units that we can. Each use of a particular unit on the top can be cancelled by one use of the same unit on the bottom. For the array we just wrote, we can cancel: “ounce Mg” (top and bottom), “g Mg” (top and bottom), “mole Mg” (top and bottom), and “mole (\mathrm{MgC} 1_{2})” (top and bottom). Striking things out is very satisfying because it simplifies the problem and makes it less confusing. If we strike out the matching units we just discussed, our array becomes:

Doesn’t that look so much cleaner? Now, just follow the usual procedure. Multiply all the numbers across the top, which is 1 x 28.35 x 1 x 1 x 95.21 = 2699.20. Multiply all the numbers across the bottom, which is 1 x 24.31 x 1 x 1 = 24.31. Divide the top by the bottom, which is 2699.20 / 24.31 = 111.03. The only units left on the top are “g \(\mathrm{MgC} 1_{2}\)”, so the answer becomes “111.03 g \(\mathrm{MgC} 1_{2}\)”.
We’ve solved the question! If one ounce of magnesium reacts with hydrochloric acid, it produces 95.21 grams of magnesium chloride.
We could have done all of these unit conversions individually, and then combined them all in pairs, and eventually arrived at the same answer. But dimensional analysis is so much easier! We just draw a horizontal line and some vertical lines to make an array. We put our initial value in the upper left box. We try to cancel units that are on the top by putting those same units on the bottom in the next block in the array, and we make sure that any individual column (top/bottom pair) in the array has a correct relationship.
Let’s try another example to really show how powerful dimensional analysis can be.
Sulfuric acid can react with sodium hydroxide to form water and Sodium Sulfate, according to the following equation:
If you start with 130 milligrams of sodium hydroxide, how many grams of sodium sulfate do you form during the reaction?
This is another scary-looking question, but just remember the simple steps of dimensional analysis. Start by writing down what you know in the upper left block of the array.

Hmm. That doesn’t get us very far. We know that calculations regarding chemical reactions usually require moles at some point, and we know that moles of a substance can be related to grams of that substance by using the molecular weight of the material. So, our first step should be to convert the mg of NaOH to g of NaOH. We know that 1000 mg of anything is equal to a gram of that substance, and we need to cancel out the “mg NaOH” as it’s on the top.
So, we’re going to work block by block in the array. First, we’re going to convert our milligrams to grams. Then, we can use grams to convert to moles. We can add up the atomic weights of Na + O + H from the Periodic Table to find the molecular weight of NaOH (the weight of 1 mole of NaOH). We know from the reaction that 2 moles of NaOH produce 1 mole of \(\mathrm{Na}_{2} \mathrm{SO}_{4}\). We can calculate the molecular weight of \(\mathrm{Na}_{2} \mathrm{SO}_{4}\) by adding up the individual atomic weights of the atoms in \(\mathrm{Na}_{2} \mathrm{SO}_{4}\) (found on the Periodic Table). That sounds like an awful lot, but we’re just doing one step at a time, and working our way forwards towards an answer.
Remember the general principles: put what you know in the first upper block. Try to cancel units on the top by having those same units on the bottom. Each individual column in the array needs to be a correct relation. Once you’ve cancelled all the units except the units in the last upper block, multiply all the values across the top. Multiply all the numbers across the bottom. Divide the top value by the bottom, and attach the only remaining units.
Here we go, hold on tight!
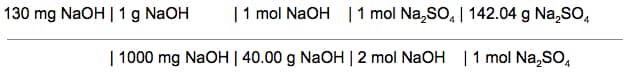
Now we get to cancel units. We can cancel “mg NaOH”, “g NaOH’, “mol NaOH”, and “mol (\mathrm{Na}{2} \mathrm{SO}{4})”. This simplifies the dimensional analysis array to:
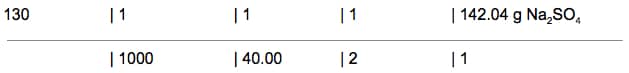
It looks so much cleaner already. Now, multiply everything along the top:
Calculation
130 x 1 x 1 x 1 x 142.04 = 18465.2
Then, multiple everything along the bottom:
1000 x 40.00 x 2 x 1 = 80000
Divide the top by the bottom:
18465.2 / 80000 = 0.231
The only units left are “g \(\mathrm{Na}_{2} \mathrm{SO}_{4}\)”, so the answer to the question is 0.231 g \(\mathrm{Na}_{2} \mathrm{SO}_{4}\). If 130 mg of NaOH reacts with sulfuric acid, it will form 0.231 grams of \(\mathrm{Na}_{2} \mathrm{SO}_{4}\).
Dimensional analysis is a powerful tool for chemists. It can take a very complicated question that would be near-impossible to do in your head and breaks it down into small, manageable parts. You only need to know the handful of general rules and principles we just discussed. Not only can you now convert any unit to any other unit very easily, but you can predict the amounts of chemicals formed when you’re given a specific amount of starting material.
Have fun using this approach to make your chemistry easier!









