In my opinion, algebra is a subject that really terrifies a lot of people. However, I can honestly say that it isn't as difficult as most people think. In order to effectively deal with algebraic expressions, it is imperative that you learn and understand the basics on this page.
Prefer to watch a video instead?
What are terms?
In order to understand anything in algebra, you have to have an understanding of what a term is. Terms are the building blocks of algebraic equations, and they can be made up of numbers, variables, or a combination of both. Terms are typically separated by either addition or subtraction operators and grouped together to form more complex expressions.
To simplify an algebraic equation, you may need to manipulate each term in the equation individually. This involves changing the order of the terms, adding or subtracting terms from each other, or multiplying or dividing terms by other values. The goal is to get the equation in a form that is easier to solve.
In Algebra, a term can be composed of a number or a variable, or a number and a variable multiplied together. Generally, terms are separated by a + or - sign, or sometimes, by a divide sign.
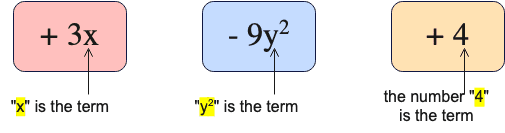
Simplifying like terms
If you want to simplify an algebraic expression that has the same terms in it, all you need to do is add or subtract them.
EXAMPLE 1 🤔 🖐️
Simplify n + n + nAll you have to do is add up all the n's:
n + n + n = 3n
EXAMPLE 2
Simplify 3s + 3s - 2sSimilar to example 1 above, combine the terms remembering to deduct the 2s:
3s + 3s - 2s = 4s
If you have a mixture of different terms, it can make it a bit more complex to simplify. You can combine 'like terms' in an algebraic expression like this, e.g. all the x terms, all the y terms, all the number terms etc.
Simplifying a common algebraic equations
Here are some examples of common algebraic equations and how they can be simplified:
Example 1
In this equation, the terms are 2x, 3y, and –5. To simplify this equation, you can rearrange the order of the terms by moving the subtraction operator and -5 to become part of the second term:
You can then combine the like terms 2x and 3y to get a new simplified equation:
Example 2
In this equation, the terms are 4x, -2, and 3x. To simplify, you can add the like terms 4x and 3x to get a new equation:
This simplifies to 7x – 2 = 9. You can then solve for x by adding 2 to each side and divide by 7:
Example 3
In this equation, the terms are 3y, 5, and -2y. To simplify, you can move the subtraction operator and -2 to become part of the third term:
This simplifies to 1y + 5 = 10. You can then subtract 5 from each side to get y alone on one side of the equation:
Remember, the goal of simplifying an equation is to make it easier to solve. In some cases, this may mean leaving the equation in a simplified form that is still somewhat complex. In other cases, you may be able to solve the equation by further simplifying each term or even combine the terms into a single value.
Ultimately, how you choose to simplify an algebraic equation will depend on the particular situation and the skills that you have mastered. With practice and patience, however, it is possible to become a master at simplifying algebraic equations and solving for their solutions!











